Relational Database의 구조
Relational Database는 표의 집합으로 이루어진다.
Students
--------------------------------------------------
| Student ID | Name | Age | Gender | Major |
--------------------------------------------------
| 001 | John Doe | 20 | Male | Biology |
| 002 | Jane Smith| 22 | Female | Physics |
| 003 | Alex Lee | 21 | Male | History |
--------------------------------------------------이 표는 학생의 정보를 담은 표이다.
- 이런 표를 Relation이라고 한다.
- Student ID, Name, Age, Gender, Major를 Attribute(Columns) 라고 한다.
- 이 Relation의 구조를 $Student = (Student ID, Name, Age, Gender, Major)$로 정의할 수 있고, 이를 Relational Schema라고 한다.
- (001, John Doe, 20, Male, Biology)와 같은 한 줄을 Tuple(Rows) 이라고 한다.
- Relation에 들어있는 Tuple의 집합을 Relational Instance라고 하고, Schema $R$에 의해 정의된 Relation Instance $r$을 $r(R)$과 같이 표현한다.
- 이 Tuple의 순서는 중요하지 않다. Relation에서 001과 002의 위치가 바뀌어도 내용이 달라지는 것은 없다.
Attributes
- 각 Attribute는 조건이 있다. (이름은 문자열이어야 하고, 학과는 학과 목록에 존재하는 문자열, 나이는 0보다 큰 숫자여야 한다.) 이러한 조건을 Domain이라고 한다.
- Attribute는 Atomic해야 한다는 조건이 있다. 즉, 분리되어서는 안 된다.
- 주소 Attribute가 도, 시, 동, 우편번호로 나뉠 수 있다면, Atomic 하지 않다.
- 값이
null인 경우도 있는데, 값을 알 수 없다는 뜻이다.
Database Schema
- Database Schema : 데이터베이스의 논리적 구조. Attribute와 Domain에 대한 내용이다.
- ex) $student(Student ID, Name, Age, Gender, Major)$
- Database Instance : 특정 시점 데이터베이스의 스냅샷.
- 어느 시점에 데이터베이스를 열면,
Students
--------------------------------------------------
| Student ID | Name | Age | Gender | Major |
--------------------------------------------------
| 001 | John Doe | 20 | Male | Biology |
| 002 | Jane Smith| 22 | Female | Physics |
| 003 | Alex Lee | 21 | Male | History |
--------------------------------------------------이런 내용을 가지고 있을 수 있다. 다른 시점에서는 내용이 변경되거나, 다른 Tuple을 가지고 있을 수도 있다.
Keys
한 스키마에 여러 Tuple이 있고, 이는 중복되어서는 안 된다. 따라서 Tuple을 구별할 방법이 필요하다.
- Attribute의 집합 중 Tuple을 구별할 수 있는 집합을 Superkey라고 한다.
- ex) {Student ID, Name}, {Student ID, Name, Major}로 학생을 구별할 수 있다.
- Superkey로 사용할 수 있는 많은 집합 중, 원소의 개수가 최소인 집합을 Candidate Key라고 한다.
- ex) {Student ID}는 1개의 원소로 학생을 모두 구분할 수 있는 Attribute이다.
- Candidate Key 여러 종류 중, 데이터베이스에서 기준으로 사용하기로 한 Key를 Primary Key라고 한다.
- 한 Relation의 Primary Key를 다른 Relation에서는 일반 Attribute로 참조할 수도 있다. 이때 참조한 Key를 Foreign Key라고 한다.
- ex) Major라는 Relation이 있다고 해보자. $Major(MajorID, Number Of Students, Number of Profs)$. 여기서 Primary Key인 $MajorID$는 $Student$에서는 일반 Attribute이다.
Schema Diagrams
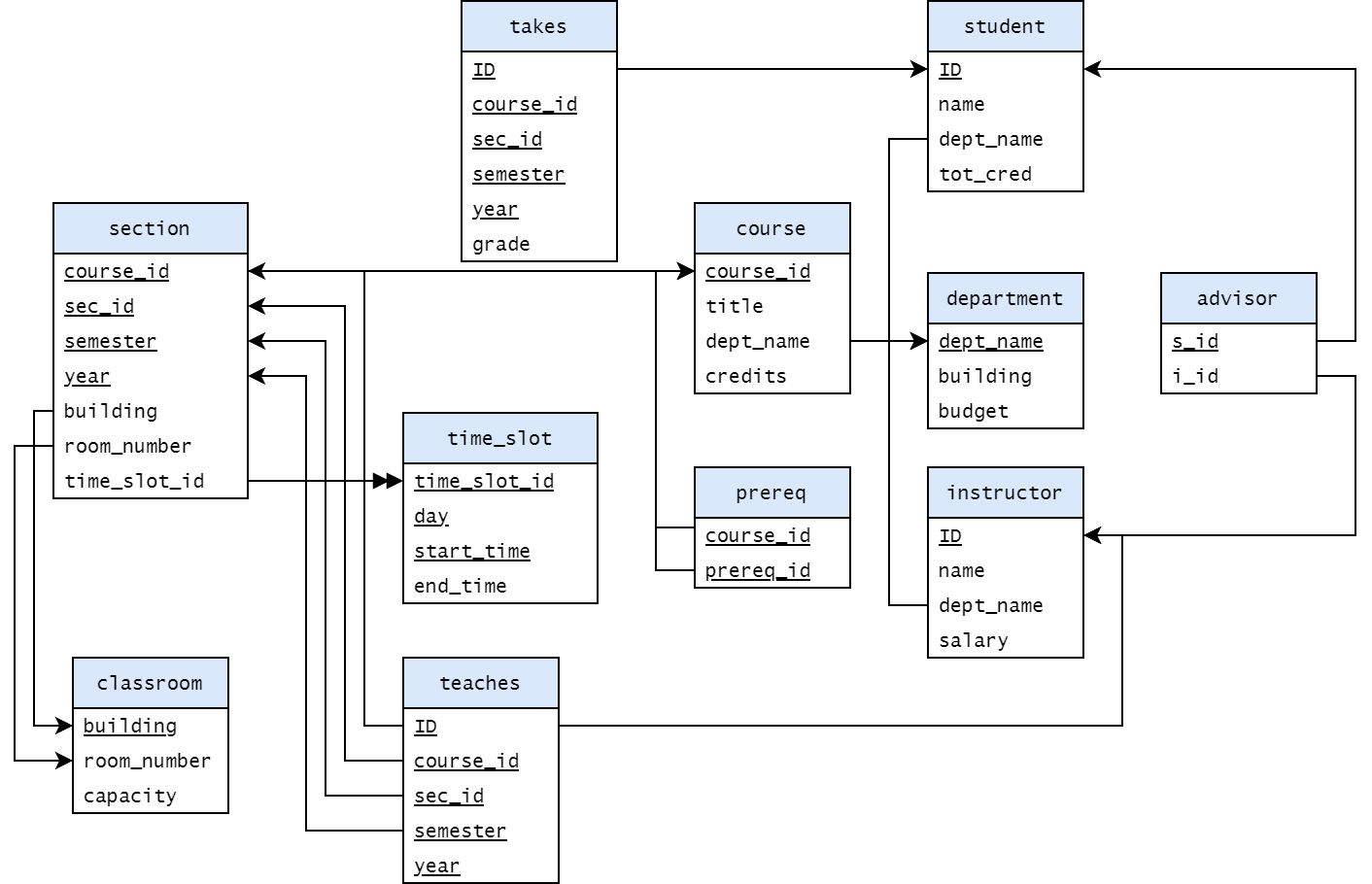
Primary Key에 밑줄, Foreign Key는 화살표로 연결한다.
Relational Query Languages
DB에서 데이터를 추출하기 위한 언어를 Query Language라고 한다.
- Imperative : 어떻게 데이터를 가져오고 조작할지 명시적으로 지정 (SQL)
- Functional : 함수를 사용해 데이터를 쿼리하고 조작 (LINQ)
- Declarative : 원하는 결과가 무엇인지만 선언
Relational Algebra
DB에서 데이터를 추출하기 위한 언어를 Query Language라고 한다.
그중 Relational Algebra는 Procedural 언어로, 데이터의 처리 과정을 명시하며, 한 개나 두 개의 Relation을 사용해 새 Relation을 얻는 방식이다.
Select $\sigma$
Select 문 $\sigma_{p}(r)$는 조건 $p$(Selection Predicate)을 만족하는 튜플을 반환한다.
ex) $\sigma_{dept\_name=Physics}(instructor)$
| ID | Name | dept_name | salary |
|------|----------------|-----------|--------|
| 3 | Sarah Johnson | Physics | 55000 |
| 8 | James White | Physics | 57000 |Selection Predicate에는 $=$, $\neq$, $>$, $\geq$, $<$, $\leq$와 같은 비교 연산자를 사용하거나,
$\wedge$(and), $\vee$(or), $\neg$(not)로 조건을 결합할 수 있다.
ex) $\sigma_{dept\_name=Physics \wedge salary > 90,000}(instructor)$
Project $\Pi$
Project문 $\Pi_{A_{1},A_{2},...,A_{k}}(r)$는 Relation의 선택한 Attribute만 반환한다.
ex) $\Pi_{ID, name, salary}(instructor)$
| ID | Name | salary |
|------|----------------|------------|
| 1 | Jane Smith | 50000 |
| 2 | John Doe | 60000 |
| 3 | Sarah Johnson | 55000 |
| 4 | Michael Brown | 52000 |
| 5 | Emily Wilson | 62000 |
| 6 | David Lee | 65000 |
| 7 | Lisa Anderson | 58000 |
| 8 | James White | 57000 |Composition
Relational Algebra의 결과는 Relation이다. 따라서 한 식의 결과가 다른 식의 인자로 들어갈 수 있다.
ex) $\Pi_{ID, name, salary}(\sigma_{dept\_name=Physics}(instructor))$
| ID | Name | salary |
|------|----------------|--------|
| 3 | Sarah Johnson | 55000 |
| 8 | James White | 57000 |Cartesian-Product $\times$
Cartesian Product는 두 Relation에서 튜플을 하나씩 뽑아 모든 경우의 쌍을 나열한 것이다.
ex) $instructor\times teaches$
| Instructor_ID | Instructor_Name | Teaches_ID | Course_ID | Course_Year |
|---------------|-----------------|------------|-----------|-------------|
| 101 | Smith | 101 | CS101 | 2023 |
| 101 | Smith | 102 | Math101 | 2024 |
| 101 | Smith | 103 | Phy101 | 2023 |
| 101 | Smith | 104 | Bio101 | 2024 |
| 102 | Johnson | 101 | CS101 | 2023 |
| 102 | Johnson | 102 | Math101 | 2024 |
| 102 | Johnson | 103 | Phy101 | 2023 |
| 102 | Johnson | 104 | Bio101 | 2024 |
| 103 | Williams | 101 | CS101 | 2023 |
| 103 | Williams | 102 | Math101 | 2024 |
| 103 | Williams | 103 | Phy101 | 2023 |
| 103 | Williams | 104 | Bio101 | 2024 |
| 104 | Jones | 101 | CS101 | 2023 |
| 104 | Jones | 102 | Math101 | 2024 |
| 104 | Jones | 103 | Phy101 | 2023 |
| 104 | Jones | 104 | Bio101 | 2024 |Join $\bowtie$
Cartesian Product는 모든 튜플 조합을 보여준다. 그러나 우리가 필요한 것은 Instructor_ID와 Teaches_ID가 일치하는 값이다. Select로 조건에 맞는 값만 선택하자.
ex) $\sigma_{instructor\_id=teaches\_id}(instructor\times teaches)$
| Instructor_ID | Instructor_Name | Teaches_ID | Course_ID | Course_Year |
|---------------|-----------------|------------|-----------|-------------|
| 101 | Smith | 101 | CS101 | 2023 |
| 102 | Johnson | 102 | Math101 | 2024 |
| 103 | Williams | 103 | Phy101 | 2023 |
| 104 | Jones | 104 | Bio101 | 2024 |이와 같은 기능을 하는 연산자가 Join이다.
Join 문 $r \bowtie_{\theta} s$는 Select 문 $\sigma_{\theta}(r \times s)$와 같다.
ex) $instructor \bowtie_{instructor\_ID=teaches\_ID} teaches$
| Instructor_ID | Instructor_Name | Teaches_ID | Course_ID | Course_Year |
|---------------|-----------------|------------|-----------|-------------|
| 101 | Smith | 101 | CS101 | 2023 |
| 102 | Johnson | 102 | Math101 | 2024 |
| 103 | Williams | 103 | Phy101 | 2023 |
| 104 | Jones | 104 | Bio101 | 2024 |Union $\cup$
Union 문 $r\cup s$는 두 Relation $r$과 $s$의 합집합을 반환한다.
Union을 쓰기 위해선 조건이 있는데,
- 합치려는 두 Relation의 Attribute의 개수가 같아야 하고,
- 합쳐지는 Attribute의 Domain이 서로 호환되어야 한다.
ex) $\Pi_{course\_ID}(\sigma_{semester=Fall \wedge year=2023}(section)) \cup \Pi_{course\_ID}(\sigma_{semester=Spring \wedge year=2024}(section))$
| Course_ID |
|-----------|
| CS101 |
| Phy101 |
| CS102 |
| Phy102 |
| Math101 |
| Bio101 |
| Math102 |
| Bio102 |Set Intersection
교집합 $r \cap s$은 두 Relation에 모두 속한 결과만 반환한다.
마찬가지로
- 두 Relation의 Attribute의 개수가 같고,
- 합쳐지는 Attribute의 Domain이 서로 호환되어야 한다.
ex) $\Pi_{course\_ID}(\sigma_{semester=Fall \wedge year=2023}(section)) \cap \Pi_{course\_ID}(\sigma_{semester=Spring \wedge year=2024}(section))$
| Course_ID |
|-----------|
| CS101 |Set Difference
차집합 $r-s$는 $r$에는 있지만 $s$에는 없는 결과를 반환한다.
이것도
- 두 Relation의 Attribute의 개수가 같고,
- 합쳐지는 Attribute의 Domain이 서로 호환되어야 한다.
ex) $\Pi_{course\_ID}(\sigma_{semester=Fall \wedge year=2023}(section)) - \Pi_{course\_ID}(\sigma_{semester=Spring \wedge year=2024}(section))$
| Course_ID |
|-----------|
| Phy102 |
| Math101 |
| Bio102 |Assignment
변수에 값을 저장하듯, Relational algebra의 결과를 변수로 써 다른 연산 때 더 가독성 있게 사용하고 싶은 경우 Assignment를 사용할 수 있다.
$A \leftarrow \sigma_{p}(r)$과 같이 $\sigma_{p}(r)$의 결과를 $A$로 지정할 수 있다.
ex)
$Physics \leftarrow \sigma_{dept_name=Physics}(instructor)$
$Music \leftarrow \sigma_{dept_name=Music}(instructor)$
$Physics \cup Music$
Rename
이름이 중복되는 등의 이유로 특정 Relation이나 Relation의 Attribute의 이름을 변경해야 할 수도 있다.
$\rho_{X}(E)$로 $E$를 $X$로 Rename할 수 있다.
또는,
$\rho_{X(A1, A2,...,An)}(E)$으로 속성을 Rename 할 수도 있다.